Leetcode 201-300
206. Reverse Linked List (Easy)¶
Reverse a singly linked list.
ListNode* reverseList(ListNode* head) {
if (head == NULL || head->next == NULL) return head;
ListNode *prev = NULL, *node = head, *next = NULL;
while (true) {
next = node->next;
node->next = prev;
if (next == NULL) return node;
prev = node;
node = next;
}
}
207. Course Schedule (Medium)¶
There are a total of n courses you have to take, labeled from 0 to n-1.
即判断一个有向图有没有环
思路
DFS，看过程中有没有后向边，即v正在访问
bool dfs(unordered_map<int, vector<int> >& e, unordered_map<int, int>& color, int u) {
color[u] = 1;
if (!e.count(u)) {
color[u] = 2;
return true;
}
for (auto v : e[u])
if (color[v] == 0 && !dfs(e, color, v)) return false;
else if (color[v] == 1) return false;
color[u] = 2;
return true;
}
bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
unordered_map<int, vector<int> > e;
unordered_map<int, int> color;
for (auto p : prerequisites) {
if (!color.count(p.first)) color[p.first] = 0;
if (!color.count(p.second)) color[p.second] = 0;
e[p.second].push_back(p.first);
}
for (auto it : color) if (color[it.second] == 0 && !dfs(e, color, it.first)) return false;
return true;
}
208. Implement Trie (Prefix Tree) (Medium)¶
Implement a trie with insert, search, and startsWith methods.
Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // returns true trie.search("app"); // returns false trie.startsWith("app"); // returns true trie.insert("app"); trie.search("app"); // returns true
思路
完成一棵前缀树即可
class Trie {
struct Node {
vector<Node*> next;
char c;
bool tail;
Node(char c) : c(c), tail(0), next(vector<Node*>(26, NULL)) {}
};
public:
vector<Node*> heads;
/** Initialize your data structure here. */
Trie() {
this->heads = vector<Node*>(26, NULL);
}
/** Inserts a word into the trie. */
void insert(string word) {
if (heads[word[0] - 'a'] == NULL) heads[word[0] - 'a'] = new Node(word[0]);
Node *ptr = heads[word[0] - 'a'];
for (int i = 1; i < word.size(); i ++) {
char c = word[i];
if (ptr->next[c-'a'] == NULL) ptr->next[c-'a'] = new Node(c);
ptr = ptr->next[c-'a'];
}
ptr->tail = 1;
}
/** Returns if the word is in the trie. */
bool search(string word) {
if (heads[word[0] - 'a'] == NULL) return NULL;
Node* ptr = heads[word[0] - 'a'];
for (int i = 1; i < word.size(); i ++) {
char c = word[i];
ptr = ptr->next[c - 'a'];
if (ptr == NULL) return false;
}
return ptr->tail;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
if (heads[prefix[0] - 'a'] == NULL) return NULL;
Node* ptr = heads[prefix[0] - 'a'];
for (int i = 1; i < prefix.size(); i ++) {
char c = prefix[i];
ptr = ptr->next[c - 'a'];
if (ptr == NULL) return false;
}
return true;
}
};
210. Course Schedule II (Medium)¶
给出一些相互依赖的课程关系，返回一个可能的修课顺序，如果不存在，返回空集
思路
拓扑排序即可
class Solution {
public:
bool dfs(const vector<vector<int>>& graph, vector<int>& color, vector<int>& result, int node, int& rank) {
color[node] = 1;
for (int v : graph[node]) {
if (color[v] == 0) {
if (!dfs(graph, color, result, v, rank)) return false;
}
else if (color[v] == 1) return false;
}
color[node] = 2;
result[rank - 1] = node; rank --;
return true;
}
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> result(numCourses, -1);
vector<int> color(numCourses, 0);
vector<vector<int>> graph(numCourses, vector<int>());
for (auto& edge : prerequisites) graph[edge[1]].push_back(edge[0]);
int rank = numCourses;
for (int i = 0; i < numCourses; i ++)
if (color[i] == 0)
if (!dfs(graph, color, result, i, rank)) return {};
return result;
}
};
212. Word Search II (Hard)¶
class Solution {
private:
class TreeNode {
public:
vector<TreeNode*> children;
char c;
bool end;
TreeNode(char c) : c(c), end(false), children(vector<TreeNode*>(26, nullptr)) {}
};
public:
void recursion(vector<vector<char>>& board, int i, int j, int n, int m, TreeNode* node, vector<string>& res, string& s) {
if (node->end) res.push_back(s);
auto func = [&board, n, m, node, &s, &res, this](int i, int j) {
if (i < 0 || i >= n || j < 0 || j >= m || board[i][j] == '-') return;
TreeNode* next = node->children[(board[i][j] - 'a')];
if (next == nullptr) return;
char temp = '-';
swap(board[i][j], temp);
string ss = s + temp;
recursion(board, i, j, n, m, next, res, ss);
swap(board[i][j], temp);
};
func(i - 1, j);
func(i + 1, j);
func(i, j - 1);
func(i, j + 1);
}
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
if (board.size() == 0 || words.size() == 0 || board[0].size() == 0) return {};
TreeNode* root = new TreeNode('$');
for (auto& word : words) {
TreeNode* node = root;
for (int i = 0; i < word.size(); i ++) {
int rank = (word[i] - 'a');
if (node->children[rank] == nullptr)
node->children[rank] = new TreeNode(word[i]);
node = node->children[rank];
}
node->end = true;
}
vector<string> res;
int n = board.size(), m = board[0].size();
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j ++) {
int rank = (board[i][j] - 'a');
if (root->children[rank] != nullptr) {
char temp = '-';
swap(temp, board[i][j]);
string s = "";
s += temp;
recursion(board, i, j, n, m, root->children[rank], res, s);
swap(temp, board[i][j]);
}
}
}
unordered_map<string, int> dict;
vector<string> result;
for (auto& s : res) {
if (!dict.count(s)) result.push_back(s);
dict[s] ++;
}
return result;
}
};
改进如下，将word直接存储在叶子节点上，然后访问到一次后置为空即可，这样时间可以从150ms上下降到44ms(99.25%)
struct TrieNode {
TrieNode* children[26] = {nullptr};
string word;
};
class Solution {
public:
void recursion(vector<vector<char>>& board, int i, int j, int n, int m, \
TrieNode* node, vector<string>& res) {
if (i < 0 || i >= n || j < 0 || j >= m || board[i][j] == '-') return;
if (node->children[(board[i][j] - 'a')] == nullptr) return;
node = node->children[(board[i][j] - 'a')];
if (node->word != "") {
res.push_back(node->word);
node->word = "";
}
char c = board[i][j];
board[i][j] = '-';
recursion(board, i - 1, j, n, m, node, res);
recursion(board, i + 1, j, n, m, node, res);
recursion(board, i, j - 1, n, m, node, res);
recursion(board, i, j + 1, n, m, node, res);
board[i][j] = c;
}
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
if (board.size() == 0 || words.size() == 0 || board[0].size() == 0) return {};
TrieNode* root = new TrieNode();
for (auto& word : words) {
TrieNode* node = root;
for (int i = 0; i < word.size(); i ++) {
int rank = (word[i] - 'a');
if (node->children[rank] == nullptr)
node->children[rank] = new TrieNode();
node = node->children[rank];
}
node->word = word;
}
vector<string> res;
int n = board.size(), m = board[0].size();
for (int i = 0; i < n; i ++)
for (int j = 0; j < m; j ++)
recursion(board, i, j, n, m, root, res);
return res;
}
};
215. Kth Largest Element in an Array (Medium)¶
找到一个array中第k大的数
快排
partition后看pivot是否是第k个，如果不是选择走左边还是右边，因为这里只需要执行一边，可以用迭代来写
快排时间复杂度为O(N)，因为每次丢掉一半，递归树只有一侧，时间复杂度为
N+N/2+N/4+...+1=2N
int findKthLargest(vector<int>& nums, int k) {
int left = 0, right = nums.size() - 1;
while (true) {
int r = right, pivot = nums[left];
for (int i = right; i > left; i --)
if (nums[i] <= pivot) swap(nums[r --], nums[i]);
swap(nums[left], nums[r]);
if (r == k - 1) return nums[r];
else if (r > k - 1) right = r - 1;
else left = r + 1;
}
}
优先级队列
时间复杂度为O(Nlogk)
比较直接的想法，连续扫描k次数组时间复杂度为O(kN)
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, std::vector<int>, greater<int> > pq;
for (auto i : nums) {
pq.push(i);
if (pq.size() > k) pq.pop();
}
return pq.top();
}
218. The Skyline Problem (Hard)¶
天际线，有若干矩形形状的建筑，这些矩形互相重叠，求这些矩形拼在一起的轮廓
轮廓可以用关键点表示出来，即从最左端/高度为0开始画线，只有遇到关键点时，上移或下移来改变画笔高度，最终画出轮廓来，如下图
数据格式，输入矩阵为[lo, hi, height]，分别为x轴上的范围和高度，输出为所有关键点，对于下图，输入输出如下
Input: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] Output: [ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]
思路
关键点的横坐标一定是矩阵在x轴上的左节点/右节点，而对应的高度则是这个点上所有建筑的最高高度
按照这个思路，先确定关键点所有的可能位置，即矩阵的所有顶点，按照横坐标排序，然后记录当前最高高度，从左到右扫描，如果在某个节点时，最高高度发生了变化，说明这个点是关键点，则加入结果中
如上图，在x=5点最高高度没有发生变化，不是关键点，在x=7上最高高度从15变成12，可以作为关键点加入结果中
实现上，维持高度可以用multiset，可以记录多个重复高度，而每次只删除一个，同时内部红黑树可以维护高度大小顺序。 在排序时，同个位置的不同节点，应该保证左节点在右节点前面，即先在multiset里先加后删，例如两个矩阵相邻，不会出现先加[x, 0]，再加[x, h]的情况，这里将左节点的高度设为负数，即可以在sort时保证这点，默认的sort比较函数对vector会依次比较各个元素，直到某个元素不同时小的在前
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
vector<vector<int>> points, res;
for (auto& b : buildings) {
points.push_back({b[0], -b[2]});
points.push_back({b[1], b[2]});
}
sort(points.begin(), points.end());
multiset<int> heights;
heights.insert(0);
int prev = 0, cur = 0;
for (auto& point : points) {
if (point[1] < 0) heights.insert(-point[1]);
else heights.erase(heights.find(point[1]));
cur = *heights.rbegin();
if (cur != prev) {
res.push_back({ point[0], cur });
prev = cur;
}
}
return res;
}
221. Maximal Square (Medium)¶
Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
Input: 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 Output: 4
解法一
和之前85一样的思路，每一行记录往上连续1个数，然后用栈计算length，再计算面积
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
vector<int> heights(matrix[0].size()+1, 0);
int mx = 0;
for (int i = 0; i < matrix.size(); i ++) {
for (int j = 0; j < matrix[0].size(); j ++) heights[j] = (matrix[i][j] == '1') ? 1+heights[j] : 0;
stack<int> s;
int ptr = 0;
while (ptr < heights.size()) {
if (s.empty() || heights[ptr] >= heights[s.top()]) s.push(ptr ++);
else {
int height = heights[s.top()];
s.pop();
int length = s.empty() ? ptr : ptr - 1 - s.top();
mx = max(mx, min(length, height) * min(length, height));
}
}
}
return mx;
}
解法二 DP
dp[i][j] = min(dp[i-1][j], min(dp[i-1][j-1], dp[i][j-1]))
实际复杂度和之前一样
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
vector<vector<int> > dp(matrix.size()+1, vector<int>(matrix[0].size()+1, 0));
int mx = 0;
for (int i = 1; i <= matrix.size(); i ++)
for (int j = 1; j <= matrix[0].size(); j ++)
if (matrix[i-1][j-1] == '1') {
dp[i][j] = min(dp[i-1][j], min(dp[i][j-1], dp[i-1][j-1])) + 1;
mx = max(dp[i][j], mx);
}
return mx * mx;
}
222. Count Complete Tree Nodes (Medium)¶
Given a complete binary tree, count the number of nodes.
思路
BFS思路，层次遍历即可
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
deque<TreeNode*> q;
q.push_back(root);
int res = 0;
while (!q.empty()) {
int s = q.size();
res += s;
for (int i = 0; i < s; i ++) {
auto node = q.front();
q.pop_front();
if (node->left != nullptr) q.push_back(node->left);
if (node->right != nullptr) q.push_back(node->right);
}
}
return res;
}
223. Rectangle Area (Medium)¶
给出两个矩形，求两个矩形的总覆盖面积，矩形由左下角和右上角坐标定义，长和宽都和坐标轴平行
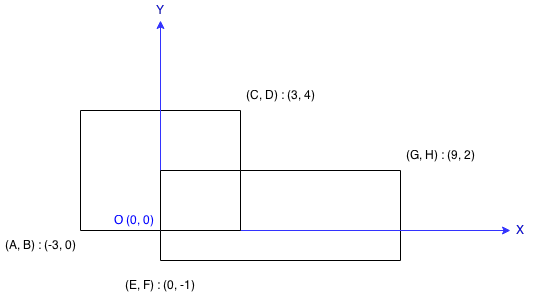
思路
重点是如何求重叠面积，这里重叠矩形的左下角[A, B]和右上角[C, D]里的四个坐标，都是由原来两个矩形的坐标组成的
比如如果有重叠矩形，左下角横坐标一定是两个矩形左下角横坐标的较大值，右上角横坐标一定是两个矩形右上角横坐标的较小值，同时判断得出的左下角横坐标是否小于右上角横坐标，即可以确定是否存在重叠矩形
int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
int left = max(A,E), right = max(min(C,G), left);
int bottom = max(B,F), top = max(min(D,H), bottom);
return (C - A) * (D - B) - (right - left) * (top - bottom) + (G - E) * (H - F);
}
224. Basic Calculator (Hard)¶
算术式求解，包含括号、数字，符号只包含加减
Input: "(1+(4+5+2)-3)+(6+8)" Output: 23
思路
可以先转换为逆波兰式，然后对逆波兰式求解，这是通用解法
但本题所要求的式子其实很简单，可以有更简洁的解法
先考虑不带括号只有加减的式子，那么因为没有优先级区别，每次读完一个数字，对前面求和即可，只需要记录前面的结果cur和当前的运算符号op。如1-2+3，读到-时，已经得到了数字1，那么cur为1，op更新为减号，下次读到+，cur更新为1-2=-1，op更新为加号，读完全式后返回-1+3=2即可
那么加入括号后，等于要先计算一下中间的式子，这里可以递归来做，但更简单的是用一个栈来暂存一下之前的数值，然后来计算括号里面的式子，计算完后再继续之前的运算
如1-2+(3-4)+5这个式子，在计算到左括号时，res=-1，op='+'，将两者都推入栈中，然后初始化为0和+，计算括号里面的式子。在遇到右括号时，得到的结果cur=-1，这时将栈中缓存的结果推出，和现在的结果一起运算：-1 + -1=-2，此时op没有值，但因为右括号紧跟着一定是运算符，到时候再更新即可
代码如下，因为op只有两种情况，所以就表示为取值1或-1的整数，这样可以和结果存在一个栈中，另外注意在遇到符号时，num要初始化为0
int calculate(string s) {
int sign = 1, cur = 0, num = 0;
stack<int> buf;
for (char c : s) {
if (c == ' ') continue;
if (c >= '0' && c <= '9') num = 10 * num + (c - '0');
else if (c == '(') {
buf.push(cur);
buf.push(sign);
cur = 0;
sign = 1;
} else if (c == ')') {
cur += sign * num;
num = 0;
cur *= buf.top(); buf.pop();
cur += buf.top(); buf.pop();
} else if (c == '+' || c == '-') {
cur += sign * num;
sign = (c == '+') ? 1 : -1;
num = 0;
}
}
return cur + sign * num;
}
226. Invert Binary Tree (Easy)¶
Invert a binary tree.
4 / \ 2 7 / \ / \ 1 3 6 94 / \ 7 2 / \ / \ 9 6 3 1
思路
递归即可
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
TreeNode *l = invertTree(root->left), *r = invertTree(root->right);
root->right = l;
root->left = r;
return root;
}
227. Basic Calculator II (Medium)¶
计算算术式的值，算术式包含数字，符号为加减乘除
Input: " 3+5 / 2 " Output: 5
思路
同样可以用逆波兰式求解
不过也可以直接计算，保存以下几个值
- res: 前面已求值的式子的结果
- cur: 当前正在求值的部分结果
- num: 当前解析的数字
- op: 上一个符号
在解析完一个数字(遇到运算符或到达式子末尾)后
- 根据上一个符号更新cur的值，如
2*3，在解析完3后，cur=2，op='*'，这时cur更新为2*3=6 - 如果遇到的符号是加减号或者式子已经到达末尾，那么之前部分可以加入到
res中，同时cur置为0，只有是乘除号的时候，这部分数值还需要考虑后面的数字 - 更新
op(如果遇到的是符号)，num置为0
代码如下
int calculate(string s) {
long long cur = 0, res = 0, num = 0;
char op = '+';
for (int i = 0; i < s.size(); i ++) {
char c = s[i];
if (c >= '0' && c <= '9') {
num *= 10;
num += (c - '0');
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == s.size() - 1) {
switch (op) {
case '+':
cur += num;
break;
case '-':
cur -= num;
break;
case '*':
cur *= num;
break;
case '/':
cur /= num;
break;
}
if (c == '+' || c == '-' || i == s.size() - 1) {
res += cur;
cur = 0;
}
op = c;
num = 0;
}
}
return res;
}
230. Kth Smallest Element in a BST (Medium)¶
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
Input: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 Output: 1
思路
先在左节点找第k小，如果找到直接返回，没找到则看root是不是恰好是第k个，不然就在右节点里找
void recursion(int& result, int& k, TreeNode* root) {
if (root == nullptr) return;
recursion(result, k, root->left);
k --;
if (k == 0) result = root->val;
if (k <= 0) return;
return recursion(result, k, root->right);
}
int kthSmallest(TreeNode* root, int k) {
int result = 0;
recursion(result, k, root);
return result;
}
233. Number of Digit One (Hard)¶
Given an integer n, count the total number of digit 1 appearing in all non-negative integers less than or equal to n.
给一个正整数n，算从1到n所有数里出现1的个数Input: 13 Output: 6 Explanation: Digit 1 occurred in the following numbers: 1, 10, 11, 12, 13.
思路
分数位统计，个数上的1每10位出现一次，所以n % 10即可，之后每一位也是，但十位上是每隔100次出现1，每次连续出现10次，百位亦然
所以从个位开始考察，每次除以10再乘以这位的进制，即是1的数量
但这里要注意的是当这位不为0的时候，要单独计算，个位又分为是否是1，如果不是1，那么加上rank，如果是1，则要看后面数字是多少，是多少就会重复多少次
代码如下
int countDigitOne(int n) {
int m = n, num = 0;
long long rank = 1;
while (m > 0) {
if (m % 10 > 1) num += rank;
else if (m % 10 == 1) num += (n % rank + 1);
num += (m / 10) * rank;
rank *= 10;
m /= 10;
}
return num;
}
234. Palindrome Linked List (Easy)¶
判断一个链表是否是回文串
思路
先算长度，然后拆一半下来reverse，与剩下的半段即可
ListNode* reverseList(ListNode* head) {
ListNode* rank = NULL;
ListNode* temp = head;
if (head != NULL) rank = head->next;
while (rank != NULL) {
ListNode* tt = rank->next;
rank->next = temp;
temp = rank;
rank = tt;
}
if (head != NULL) head->next = NULL;
return temp;
}
bool isPalindrome(ListNode* head) {
int length = 0;
for (ListNode* node = head; node != NULL; node = node->next) length++;
if (length < 2) return true;
int mid = (length % 2) ? (length+1)/2 : length/2;
ListNode* head0 = head;
for (int rank = 0; rank != mid; head0 = head0->next, rank ++) ;
head0 = reverseList(head0);
ListNode* head1 = head;
for (ListNode* head1 = head; head0 != NULL; head1=head1->next, head0=head0->next)
if (head1->val != head0->val) return false;
return true;
}
236. Lowest Common Ancestor of a Binary Tree (Medium)¶
给一棵树，和两个节点，返回这两个节点的最小公共祖先
如下图，5和1的最小祖先是3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.
思路
递归来做，这里不太好想条件，其实递归找到一个p和q就可以返回，这里很关键，然后判断左右是否都在
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root==NULL || root==p || root==q) return root;
TreeNode* leftSide = lowestCommonAncestor(root->left, p, q);
TreeNode* rightSide = lowestCommonAncestor(root->right, p, q);
if (leftSide != NULL && rightSide != NULL) return root;
if (leftSide == NULL)return rightSide;
return leftSide;
}
238. Product of Array Except Self (Medium)¶
给一个数组，对每个位置求除该数外其余数之积，不用触发
思路
要求的积即为这个数左边数乘积和右边数乘积之积，扫描两遍即可
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> result(nums.size(), 1);
if (nums.size() == 0) return result;
result[0] = nums[0];
for (int i = 1; i < result.size() - 1; i ++) result[i] = nums[i] * result[i-1];
int product = 1;
for (int i = result.size() - 1; i >= 0; i --) {
result[i] = (i > 0) ? result[i-1]*product : product;
product *= nums[i];
}
return result;
}
239. Sliding Window Maximum (Hard)¶
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.
Input: nums = [1,3,-1,-3,5,3,6,7], and k = 3 Output: [3,3,5,5,6,7] Explanation: Window position Max --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
思路
用一个辅助deque来保存窗口内最大值，思想就是当后面出现一个更大的数时，前面保存的数都作废，否则就加到deque后面，同时如果滑出窗口的数还在用，也要从deque中摘除出去
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> result;
deque<int> temp;
for (int i = 0; i < nums.size(); i ++) {
while (!temp.empty() && temp.back() < nums[i]) temp.pop_back();
temp.push_back(nums[i]);
if (i >= k && nums[i-k] == temp.front()) temp.pop_front();
if (i >= k - 1) result.push_back(temp.front());
}
return result;
}
240. Search a 2D Matrix II (Medium)¶
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Given target = 5, return true.[ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]Given target = 20, return false.
思路
从左下角出发，向右数字变大，向上数字变小，如果target存在，沿着这两个方向一定可以找到
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
int i = matrix.size() - 1, j = 0;
while (i >= 0 && j < matrix[0].size()) {
if (matrix[i][j] == target) return true;
else if (matrix[i][j] < target) j ++;
else i --;
}
return false;
}
253. Meeting Rooms II (Medium)¶
Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required.
For example, Given [[0, 30],[5, 10],[15, 20]], return 2.
思路
整体思路就是看一个会议开始前，之前有没有结束的会议，如果有就不用加会议室，不然就要新加会议室
解法一
用map来存start和end，start对应1，end对应-1，最后按照key顺序加起来，过程中记录最大值即为答案
int minMeetingRooms(vector<Interval>& intervals) {
map<int, int> m;
for (auto a : intervals) {
++m[a.start];
--m[a.end];
}
int rooms = 0, res = 0;
for (auto it : m) {
res = max(res, rooms += it.second);
}
return res;
}
解法二
把start和end放在一个vector里面，sort一下，然后从头扫描start和end，如果start小于当前end，加一，否则两者都往后移
int minMeetingRooms(vector<Interval>& intervals) {
vector<int> starts, ends;
int res = 0, endpos = 0;
for (auto a : intervals) {
starts.push_back(a.start);
ends.push_back(a.end);
}
sort(starts.begin(), starts.end());
sort(ends.begin(), ends.end());
for (int i = 0; i < intervals.size(); ++i) {
if (starts[i] < ends[endpos]) ++res;
else ++endpos;
}
return res;
}
解法三
先以start对所有时间对排序，用一个小顶堆来记录end，然后依次访问时间对，有两种情况，当前start大于等于最小的end，则入堆同时将堆顶元素推出，否则只入堆
最后堆大小即为答案
int minMeetingRooms(vector<Interval>& intervals) {
sort(intervals.begin(), intervals.end(), [](const Interval &a, const Interval &b){return a.start < b.start;});
priority_queue<int, vector<int>, greater<int>> q;
for (auto a : intervals) {
if (!q.empty() && q.top() <= a.start) q.pop();
q.push(a.end);
}
return q.size();
}
265. Paint House II (Hard)¶
有
n个房子，每个房子可以涂k种颜色，每个房子涂颜色的cost不一样，记作cost[n][k]，相邻房子不能涂一种颜色，求涂完所有房子的最低成本
Input: [[1,5,3],[2,9,4]]
Output: 5
Explanation: Paint house 0 into color 0, paint house 1 into color 2.
Minimum cost: 1 + 4 = 5;
Or paint house 0 into color 2, paint house 1 into color 0. Minimum cost: 3 + 2 = 5.
思路
对第m层来说，只需要前m-1层染色代价的最小值和倒数第二小值，再记录前一层的颜色，然后这层其它颜色的代价和前m-1层最小值相加，和前一层重复的颜色和倒数第二小值相加，从中取最小值即可
代码如下，可以注意下更新最小值和第二小值代码，两次比较即可
int minCostII(vector<vector<int>>& costs) {
if (costs.size() == 0 || costs[0].size() == 0) return 0;
int min1 = 0, min2 = 0, idx = -1;
for (int i = 0; i < costs.size(); i ++) {
int mn1 = INT_MAX, mn2 = INT_MAX, temp, tempIdx;
for (int j = 0; j < costs[0].size(); j ++) {
temp = costs[i][j] + (j == idx ? min2 : min1);
if (temp < mn1) {
mn2 = mn1; mn1 = temp; tempIdx = j;
}
else if (temp < mn2) mn2 = temp;
}
min1 = mn1; min2 = mn2; idx = tempIdx;
}
return min1;
}
272. Closest Binary Search Tree Value II (Hard)¶
给一棵非空的二分搜索树以及一个
target值，找k个二分搜索树中最接近这个值的节点Input: root = [4,2,5,1,3], target = 3.714286, and k = 2 4 / \ 2 5 / \ 1 3 Output: [4,3]
思路
中序遍历，将小于target的放在一个栈里，大于target的放在一个队列里，然后比较两者的开头元素哪个小即可，代码如下
vector<int> closestKValues(TreeNode* root, double target, int k) {
stack<int> ls;
deque<int> rs;
stack<TreeNode*> s;
TreeNode* ptr = root;
while (ptr != nullptr || !s.empty()) {
while (ptr != nullptr) {
s.push(ptr);
ptr = ptr->left;
}
if (!s.empty()) {
ptr = s.top();
if (ptr->val < target) ls.push(ptr->val);
else rs.push_back(ptr->val);
s.pop();
ptr = ptr->right;
}
}
vector<int> result;
while (result.size() < k && (rs.size() + ls.size() > 0)) {
bool lflag = false, rflag = false;
if (ls.empty()) rflag = true;
else if (rs.empty()) lflag = true;
else {
double dis1 = (rs.front() - target) * (rs.front() - target);
double dis2 = (ls.top() - target) * (ls.top() - target);
if (dis1 < dis2) rflag = true;
else lflag = true;
}
if (lflag) {
result.push_back(ls.top());
ls.pop();
} else if (rflag) {
result.push_back(rs.front());
rs.pop_front();
}
}
return result;
}
273. Integer to English Words (Hard)¶
将一个非负int整数转换为英文表示，只写数字，不考虑
andInput: 123 Output: "One Hundred Twenty Three" Input: 1234567891 Output: "One Billion Two Hundred Thirty Four Million Five Hundred Sixty Seven Thousand Eight Hundred Ninety One"
思路
int最大正数2^{31}-1 \approx 2*10^9，所以考虑Billion, Million, Thousand这几个量级即可，每个量级上将1-999的数字表示出来，加上量级即可
注意需要对0做特判，写的时候要多注意细节
class Solution {
private:
string digits[9] = {"One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
string tens[10] = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
string hs[8] = {"Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
string parse(int num) {
string res = "";
if (num >= 100) res = " " + digits[num/100 - 1] + " Hundred";
num %= 100;
if (num >= 10) {
if (num < 20) {
res = res + " " + tens[num - 10];
return res.substr(1);
}
else res += (" " + hs[num/10 - 2]);
}
num %= 10;
if (num > 0) res += (" " + digits[num - 1]);
return res.substr(1);
}
public:
string numberToWords(int num) {
if (num == 0) return "Zero";
string magnitude[4] = {"Billion", "Million", "Thousand", ""};
int orders[4] = { 1000000000, 1000000, 1000, 1 };
string res = "";
int order = 1000000000;
for (int i = 0; i < 4; i ++) {
if (num >= orders[i]) {
res += (" " + parse(num/orders[i]));
if (i < 3) res += (" " + magnitude[i]);
num %= orders[i];
}
}
return res.substr(1);
}
};
279. Perfect Squares (Medium)¶
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.
Input: n = 12 Output: 3 Explanation: 12 = 4 + 4 + 4.
class A {
public:
void m() {
static int num = 0;
num ++;
cout << num << '\n';
}
};
int main() {
A a;
a.m(); // 1
a.m(); // 2
a.m(); // 3
}
解法一 DP
dp[0-n]，dp[i]表示数字n对应的最小平方数个数
int numSquares(int n) {
static vector<int> dp = {0};
while (dp.size() <= n) {
int m = dp.size();
int mx = m;
for (int i = 1; i*i <= m; i ++)
mx = min(mx, dp[m-i*i]+1);
dp.push_back(mx);
}
return dp[n];
}
四平方和定理 每个正整数均可表示为4个整数的平方和
282. Expression Add Operators (Hard)¶
给一串数字，向其中加入+ - *运算符号，使得式子结果等于target
Input: num = "123", target = 6 Output: ["1+2+3", "1*2*3"]
思路
深搜来遍历，这里需要注意的技巧是记录上一个+或-时加上的数，然后在遇到乘号时，先对应减或加上这个数，然后再乘，如下，记下-2，然后在遇到乘法时先加上2，然后进行之后的深搜遍历
1 - 2 = -1 prev = -2
1 - 2 * 3 = -1 + 2 - 2 * 3 = -5
vector<string> result;
void helper(const string& num, int begin, int target, long value, long prevVal, string& s, int len) {
if (begin == num.size()) {
if (target == value) result.push_back(s.substr(0, len));
return;
}
long numValue = 0;
int opPos = len;
if (begin > 0) len ++;
for (int i = begin; i < num.size(); i ++) {
if (num[begin] == '0' && i > begin) return;
numValue *= 10; numValue += (num[i] - '0');
s[len ++] = num[i];
string substr = num.substr(begin, i - begin + 1);
if (begin > 0) {
s[opPos] = '+'; helper(num, i + 1, target, value + numValue, numValue, s, len);
s[opPos] = '-'; helper(num, i + 1, target, value - numValue, -numValue, s, len);
s[opPos] = '*'; helper(num, i + 1, target, value - prevVal + prevVal * numValue, prevVal * numValue, s, len);
}
else helper(num, i + 1, target, numValue, numValue, s, len);
}
}
vector<string> addOperators(string num, int target) {
string s(num.size() * 2, '\0');
helper(num, 0, target, 0, 0, s, 0);
return result;
}
283. Move Zeroes (Easy)¶
Given an array nums, write a function to move all 0's to the end of it while maintaining the relative order of the non-zero elements.
Input: [0,1,0,3,12] Output: [1,3,12,0,0]
思路
双指针，移动即可
void moveZeroes(vector<int>& nums) {
if (nums.size() == 0) return;
int zeroPtr = 0;
while (zeroPtr < nums.size() && nums[zeroPtr] != 0) zeroPtr ++;
for (int i = 0; i < nums.size() && zeroPtr < nums.size(); i ++)
if (nums[i] != 0 && i > zeroPtr) {
swap(nums[i], nums[zeroPtr]);
while (nums[zeroPtr] != 0) zeroPtr ++;
}
}
285. Inorder Successor in BST (Medium)¶
Given a binary search tree and a node in it, find the in-order successor of that node in the BST.
The successor of a node p is the node with the smallest key greater than p.val.
求二叉树中一个点的中序遍历后继
思路
用栈来进行中序遍历，发现栈顶元素为p时，将下一个元素返回即可
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
stack<TreeNode*> s;
TreeNode *ptr = root;
bool flag = false;
while (ptr != nullptr || !s.empty()) {
while (ptr != nullptr) {
s.push(ptr);
ptr = ptr->left;
}
if (!s.empty()) {
ptr = s.top();
s.pop();
if (flag) return ptr;
if (ptr == p) flag = true;
ptr = ptr->right;
}
}
return nullptr;
}
这里应该也可以用morris来遍历输出，但一直内存溢出，不知道为什么
286. Walls and Gates (Medium)¶
一个二维数组，有三种可能值
- -1 表示墙或障碍物
- 0 表示门
- INF 即INT_MAX，表示空地
求空地到最近门的距离，如果到不了，继续填充INF即可
思路
从各个门处开始宽搜，更新距离即可
要注意已经搜过的元素不能再进入队列，这里判断元素的距离是否小于当前维护的距离即可，若小于不进行更新
void wallsAndGates(vector<vector<int>>& rooms) {
vector<vector<int>> step = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
if (rooms.size() == 0 || rooms.size() == 0) return;
int num = 0;
for (int i = 0; i < rooms.size(); i ++) {
for (int j = 0; j < rooms[0].size(); j ++) {
if (rooms[i][j] != 0) continue;
num ++;
queue<pair<int, int>> q;
q.push({i, j});
int level = 0;
while (!q.empty()) {
level ++;
int size = q.size();
while (size --) {
auto& node = q.front();
for (auto& v : step) {
int newi = node.first + v[0], newj = node.second + v[1];
if (newi < 0 || newi == rooms.size() || newj < 0 || newj == rooms[0].size()) continue;
if (rooms[newi][newj] < level) continue;
rooms[newi][newj] = min(level, rooms[newi][newj]);
q.push({newi, newj});
}
q.pop();
}
}
}
}
}
287. Find the Duplicate Number (Medium)¶
n个数里只有一个重复，找到该数
位图
因为数组中数范围是1-n，所以可以对每个bit位，统计一下从1-n正常的bit个数，然后再比较一下nums的bit个数，当后者bit个数更多时，说明重复数该位为1
这个算法前提是数组中1-n都要出现，不过leetcode上可以通过 20ms(21.37%)
int findDuplicate(vector<int>& nums) {
int res = 0;
for (int i = 0; i < 32; i ++) {
int bit = (1 << i), cnt1 = 0, cnt2 = 0;
for (int j = 0; j < nums.size(); j ++) {
if (j & bit) cnt1 ++;
if (nums[j] & bit) cnt2 ++;
}
if (cnt2 > cnt1) res += bit;
}
return res;
}
链表环
很巧妙的方法，把nums[k]看做k的下一个节点，因为有循环，所以一定会有环，而且从0开始访问，不会进入自环中，所以等价于142. Linked List Cycle II (Medium)这道题，时间为 12ms(99.81%)
int findDuplicate(vector<int>& nums) {
int fast = 0, slow = 0;
while (true) {
fast = nums[nums[fast]];
slow = nums[slow];
if (fast == slow) break;
}
slow = 0;
while (slow != fast) {
fast = nums[fast];
slow = nums[slow];
}
return fast;
}
291. Word Pattern II (Hard)¶
给一个
pattern串和一个str串，看str是否满足pattern的格式Input: pattern = "abab", str = "redblueredblue" Output: true
思路
还是深搜来遍历，不过可以利用单词长度剪枝，即每确定一个char-string的映射，计算下这样映射所得的字符串长度，看是否超过str长度
然后从pattern串开始，深搜来遍历所有组合
bool wordPatternMatch(string pattern, string str) {
vector<int> cnt(26, 0);
vector<string> dict(26, "");
for (char p : pattern) cnt[p - 'a'] ++;
unordered_set<string> words;
return helper(pattern, 0, str, 0, cnt, dict, words, pattern.size());
}
bool helper(const string& pattern, int pp, const string& str, int sp, const vector<int>& cnt, vector<string>& dict, unordered_set<string>& words, int lowerLimit) {
if (pp == pattern.size() && sp == str.size()) return true;
if (pp == pattern.size() || sp == str.size()) return false;
int rank = pattern[pp] - 'a';
string& word = dict[rank];
if (word.size() == 0) {
for (int i = sp; i < str.size(); i ++) {
word += str[i];
if (words.count(word)) continue;
int newLimit = lowerLimit + cnt[rank] * (word.size() - 1);
if (newLimit > str.size()) break;
words.insert(word);
if (helper(pattern, pp + 1, str, i + 1, cnt, dict, words, newLimit)) return true;
words.erase(word);
}
word = "";
return false;
} else {
if (str.size() < word.size() + sp) return false;
if (str.substr(sp, word.size()) != word) return false;
if (helper(pattern, pp + 1, str, sp + word.size(), cnt, dict, words, lowerLimit)) return true;
}
return false;
}
297. Serialize and Deserialize Binary Tree (Hard)¶
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
思路
用一个queue来BFS即可，注意左右孩子必须同时加入，即使一个是NULL
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if (root == NULL) return "null";
queue<TreeNode*> q;
q.push(root);
string s = "";
int realNum = 1;
while (!q.empty()) {
TreeNode *node = q.front();
q.pop();
string v = (node != NULL) ? to_string(node->val) : "null";
if (s == "") s = v;
else s = s + "=" + v;
if (node != NULL) {
realNum --;
q.push(node->left);
q.push(node->right);
if (node->left != NULL) realNum ++;
if (node->right != NULL) realNum ++;
}
if (realNum == 0) break;
}
return s;
}
TreeNode* deserialize(string data) {
if (data == "null") return NULL;
int left = 0;
string sub = data.substr(0, data.find_first_of('='));
TreeNode *root = new TreeNode(stoi(sub));
data = (data.size() > sub.size()) ? data.substr(sub.size() + 1) : "";
queue<TreeNode*> q;
q.push(root);
while (data.size() > 0) {
TreeNode* node = q.front(); q.pop();
string sub = data.substr(0, data.find_first_of('='));
TreeNode *node1 = NULL, *node2 = NULL;
if (sub != "null") node1 = new TreeNode(stoi(sub));
if (node1 != NULL) q.push(node1);
if (node != NULL) node->left = node1;
data = (data.size() > sub.size()) ? data.substr(sub.size() + 1) : "";
if (data.size() == 0) break;
sub = data.substr(0, data.find_first_of('='));
if (sub != "null") node2 = new TreeNode(stoi(sub));
if (node2 != NULL) q.push(node2);
data = (data.size() > sub.size()) ? data.substr(sub.size() + 1) : "";
if (node != NULL) node->right = node2;
if (data.size() == 0) break;
}
return root;
}
};
300. Longest Increasing Subsequence (Medium)¶
Given an unsorted array of integers, find the length of longest increasing subsequence.
求上升子序列
思路
用DP来做的话，O(N^2)时间内可以很简单做出来，即dp[i]表示以nums[i]结尾的最长上升子序列长度，对dp[i+1]，从nums[0]到nums[i]比较一下，dp[i+1]=max(dp[j]+1) where nums[j]<nums[i+1]
下面算法是O(NlogN)，具体思路为二分来更新序列，具体过程为维护一个vector，对num in nums
- 如果num小于vector首元素，首元素改为num
- 如果num大于vector尾元素，v.push_back(num)
- 如果num在中间，找到不小于num的元素，将其改为num
这样的过程不太好理解，下面以[1,3,5,2,8,4,6]为例说明一下背后思想
在扫描到6时，上升序列有如下几种
1
1 2
1 2 4
1 3 4
1 3 5
1 3 6
1 3 5 8
注意只要末尾元素确定，那么1 2 4和1 3 4两个序列一样，而长度一样时，末尾元素小的一个序列严格优于大的那个，如1 3 4和1 3 5，接下来后者的扩展前者都可以做到，因此只看前者即可
所以vector任意前i位，维护的都是目前为止长度为i且末尾元素最小的序列，最后看vector长度即可
int lengthOfLIS(vector<int>& nums) {
if (nums.size() < 2) return nums.size();
vector<int> v;
v.push_back(nums[0]);
for (int num : nums) {
if (num < v.front()) v[0] = num;
else if (num > v.back()) v.push_back(num);
else {
int l = 0, r = v.size() - 1;
while (l <= r) {
int m = (l + r) / 2;
if (v[m] >= num) r = m - 1;
else l = m + 1;
}
v[l] = num;
}
}
return v.size();
}